图的匹配

图的匹配相关概念

匹配 或是 独立边集 是一张图中不具有公共端点的边的集合。
在二分图中求匹配等价于网路流问题。

图匹配算法是信息学竞赛中常用的算法，总体分为最大匹配以及最大权匹配，先从二分图开始介绍，再进一步提出一般图的作法。

图的匹配

在图论中，假设图 $G=(V,E)$，其中 $V$ 是点集，$E$ 是边集。

一组两两没有公共点的边集 $M(M\in E)$ 称为这张图的 匹配。

定义匹配的大小为其中边的数量 $|M|$，其中边数最大的 $M$ 为 最大匹配。

当图中的边带权的时候，边权和最大的为 最大权匹配。

匹配中的边称为 匹配边，反之称为 未匹配边。

一个点如果属于 $M$ 且为至多一条边的端点，称为 匹配点，反之称为 未匹配点。

  • 极大匹配（maximal matching）：无法再增加匹配边的匹配。不一定是最大匹配。

  • 最大匹配（maximum matching or maximum cardinality matching）：匹配边数量最多的匹配。最大匹配可能有不止一个，但最大匹配的边数是确定的，而且不可能超过图中定点数的一半。

  • 最大权匹配（maximum weight matching）：加权图中，权值和最大的匹配。

  • 最大权最大匹配（maximum weight maximum cardinality matching）：匹配数最多的前提下，边权和最大的匹配。即所有最大匹配中，边权和最大的匹配。

  • 完美匹配（perfect matching）：所有点都属于匹配，同时也符合最大匹配。若图 G 为完全图且顶点数为偶数时，必然存在完美匹配。

  • 近完美匹配（near-perfect matching）：发生在图的点数为奇数，刚好只有一个点不在匹配中，扣掉此点以后的图称为 factor-critical graph。

    maximal matching

    maximal matching

    最大匹配

    maximum cardinality matching

    最大权匹配

    maximum weight matching

    最大权最大匹配

    maximum weight maximum cardinality matching

二分图匹配

bi-graph

一张二分图上的匹配称作二分匹配

设 $G$ 为二分图，若在 $G$ 的子图 $M$ 中，任意两条边都没有公共节点，那么称 $M$ 为二分图 $G$ 的一个匹配，且 $M$ 的边数为匹配数。

完美匹配

设 $G=\langle V_1, V_2, E \rangle$ 为二分图，$|V_1| \leq |V_2|$，$M$ 为 $G$ 中一个最大匹配，且 $|M|=|V_1|$，则称 $M$ 为 $V_1$ 到 $V_2$ 的完美匹配。

二分图

染色法：使用两种颜色，给图上每一点涂上颜色，使得相邻两点颜色不同

  1. 不存在奇数环、染色法不存在矛盾

  2. 匈牙利算法，匹配、最大匹配、匹配点、增广路径

  3. 最小点覆盖、最大独立集、最小路径点覆盖（最小路径重复点覆盖）

    最大匹配数=最小点覆盖=（总点数-最大独立集）=（总点数-最小路径覆盖）

染色法判断二分图

使用两种颜色，给图上每一点涂上颜色，使得相邻两点颜色不同

用一个color数组记录颜色，直接dfs即可

1
2
3
4
5
6
7
8
9
10
11
bool dfs(int u, int c) {
    color[u] = c;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (color[j] == c) return false;
        if (!color[j]) 
            if (!dfs(j, 3 - c, mid)) return false;
    }

    return true;
}

匈牙利算法

定理一：“图G中的一个匹配M是最大匹配”的充分必要条件是“G中不存在M的增广路径”。

根据定理一，匈牙利算法的核心思路是：任选一条边作为初始匹配M，然后通过寻找增广路径来扩大匹配M中边的条数，直到无法继续扩展新的边，此时M为最大匹配。其中，算法的关键在于寻找增广路径。

匈牙利算法的执行过程，以程序语言总结如下：

  1. 初始化顶点编号（1～N），令循环顶点索引 X=1
  2. 如果X>N, 结束；如果X<=N, 进入Step3
  3. 利用dfs寻找 以X为起点的增广路径，并对M进行扩展（如果没有找到，则不对M进行扩展）。X++，转Step2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
bool find(int x) {
    for (int i = 1; i <= m; i ++ ) {
        if (!st[i] && g[x][i]) {
            st[i] = true;
            int t = match[i];
            if (!t || find(t)) {
                match[i] = x;
                return true;
            }
        }
    }

    return false;
}

int main() {
    ...
    for (int i = 1; i <= n; i ++ ) {
        memset(st, 0, sizeof st);
        if (find(i)) res ++;
    }
    ...
}

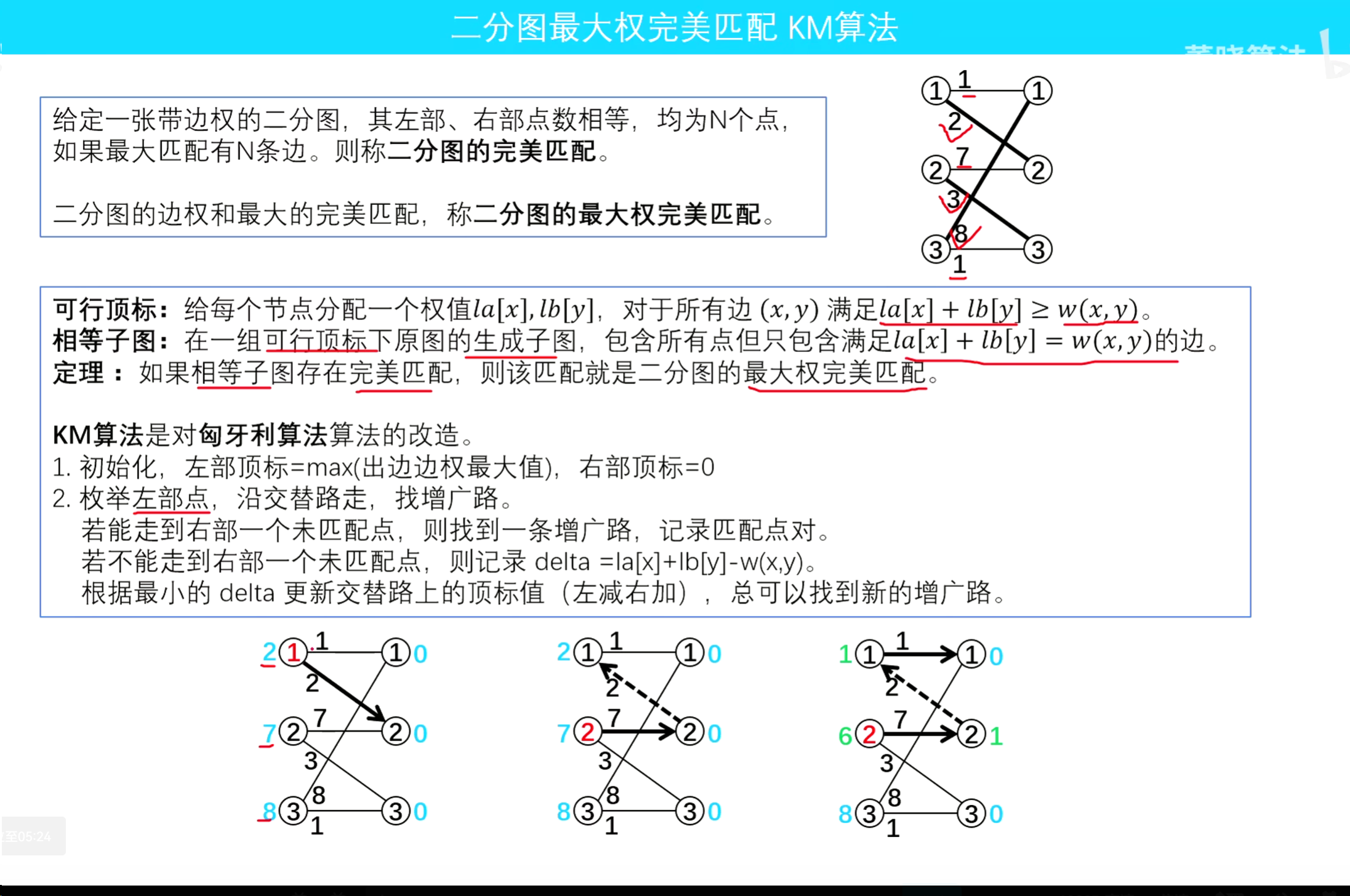
KM算法

匈牙利算法，主要在于解决无权二分图的最大匹配问题；而如果要寻找完全二分图的最大权匹配，需要用到KM算法。

image-20240418203516746

dfs算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include <bits/stdc++.h>

typedef long long LL;

const int N = 510;
const LL INF = 1e18;

int n, m;
LL g[N][N];
LL match[N];
LL slack[N], lx[N], ly[N];
bool vx[N], vy[N];

bool find(int x) {
    vy[x] = true;
    for (int i = 1; i <= n; i ++ ) {
        if (vx[i]) continue;
        LL d = lx[i] + ly[x] - g[x][i];
        if (!d) {
            vx[i] = true;
            if (!match[i] || find(match[i])) {
                match[i] = x;
                return true;
            }
        } else slack[i] = std::min(slack[i], d);
    }
    return false;
}

LL KM() {
    memset(match, 0, sizeof(match));
    memset(lx, 0, sizeof(lx));
    std::fill(ly + 1, ly + n + 1, -INF);
    for (int i = 1; i <= n; i ++ ) {
        for (int j = 1; j <= n; j ++ ) {
            ly[i] = std::max(ly[i], g[i][j]);
        }
    }
    for (int i = 1; i <= n; i ++ ) {
        std::fill(slack + 1, slack + n + 1, INF);
        while (true) {
            memset(vx, 0, sizeof(vx));
            memset(vy, 0, sizeof(vy));
            if (find(i)) break;
            LL d = INF;
            for (int j = 1; j <= n; j ++ ) {
                if (!vx[j]) d = std::min(d, slack[j]);
            }
            for (int j = 1; j <= n; j ++ ) {
                if (vy[j]) ly[j] -= d;
                if (vx[j]) lx[j] += d;
                else slack[j] -= d;
            }
        }
    }

    LL res = 0;
    for (int i = 1; i <= n; i ++ ) {
        res += g[match[i]][i];
    }

    return res;
}

int main() {
    std::cin >> n >> m;

    for (int i = 1; i <= n; i ++ ) {
        for (int j = 1; j <= n; j ++ ) {
            g[i][j] = -INF;
        }
    }

    while (m --) {
        int a, b;
        LL c;
        std::cin >> a >> b >> c;
        g[a][b] = std::max(g[a][b], c);
    }

    LL km = KM();
    std::cout << km << '\n';
    for (int i = 1; i <= n; i ++ ) {
        std::cout << match[i] << " ";
    }
    std::cout << '\n';

    return 0;
}

bfs写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
typedef long long ll;
const ll Maxn=505;
const ll inf=1e18;
ll n,m,map[Maxn][Maxn],matched[Maxn];
ll slack[Maxn],pre[Maxn],ex[Maxn],ey[Maxn];//ex,ey顶标
bool visx[Maxn],visy[Maxn];
void match(ll u)
{	
    ll x,y=0,yy=0,delta;
    memset(pre,0,sizeof(pre));
    for(ll i=1;i<=n;i++)slack[i]=inf;
    matched[y]=u;
    while(1)
    {	
        x=matched[y];delta=inf;visy[y]=1;
        for(ll i=1;i<=n;i++)
        {	
            if(visy[i])continue;
            if(slack[i]>ex[x]+ey[i]-map[x][i])
            {	
                slack[i]=ex[x]+ey[i]-map[x][i];
                pre[i]=y;
            }
            if(slack[i]<delta){delta=slack[i];yy=i;}
        }
        for(ll i=0;i<=n;i++)
        {	
            if(visy[i])ex[matched[i]]-=delta,ey[i]+=delta;
            else slack[i]-=delta;
        }
        y=yy;
        if(matched[y]==-1)break;
    }
    while(y){matched[y]=matched[pre[y]];y=pre[y];}
}
ll KM()
{	
    memset(matched,-1,sizeof(matched));
    memset(ex,0,sizeof(ex));
    memset(ey,0,sizeof(ey));
    for(ll i=1;i<=n;i++)
    {	
        memset(visy,0,sizeof(visy));
        match(i);
    }
    ll res=0;
    for(ll i=1;i<=n;i++)
        if(matched[i]!=-1)res+=map[matched[i]][i];
    return res;
}
int main()
{	
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            map[i][j]=-inf;
    for(ll i=1;i<=m;i++)
    {	
        ll u,v,w;
        scanf("%lld%lld%lld",&u,&v,&w);
        map[u][v]=w;
    }
    printf("%lld\n",KM());
    for(ll i=1;i<=n;i++)
        printf("%lld ",matched[i]);
    printf("\n");
    return 0;
}

其他图的匹配相关概念

支配集

对于无向图 $G=(V, E)$，若 $V’\subseteq V$ 且 $\forall v\in(V\setminus V’)$ 存在边 $(u, v)\in E$ 满足 $u\in V’$，则 $V’$ 是图 $G$ 的一个 **支配集 (dominating set)**。

无向图 $G$ 最小的支配集的大小记作 $\gamma(G)$。求一张图的最小支配集是 NP 困难 的。

对于有向图 $G=(V, E)$，若 $V’\subseteq V$ 且 $\forall v\in(V\setminus V’)$ 存在边 $(u, v)\in E$ 满足 $u\in V’$，则 $V’$ 是图 $G$ 的一个 **出 - 支配集 (out-dominating set)**。类似地，可以定义有向图的 **入 - 支配集 (in-dominating set)**。

有向图 $G$ 最小的出 - 支配集大小记作 $\gamma^+(G)$，最小的入 - 支配集大小记作 $\gamma^-(G)$。

边支配集

对于图 $G=(V, E)$，若 $E’\subseteq E$ 且 $\forall e\in(E\setminus E’)$ 存在 $E’$ 中的边与其有公共点，则称 $E’$ 是图 $G$ 的一个 **边支配集 (edge dominating set)**。

求一张图的最小边支配集是 NP 困难 的。

独立集

对于图 $G=(V, E)$，若 $V’\subseteq V$ 且 $V’$ 中任意两点都不相邻，则 $V’$ 是图 $G$ 的一个 **独立集 (independent set)**。

图 $G$ 最大的独立集的大小记作 $\alpha(G)$。求一张图的最大独立集是 NP 困难 的。

匹配

对于图 $G=(V, E)$，若 $E’\in E$ 且 $E’$ 中任意两条不同的边都没有公共的端点，且 $E’$ 中任意一条边都不是自环，则 $E’$ 是图 $G$ 的一个 **匹配 (matching)**，也可以叫作 **边独立集 (independent edge set)**。如果一个点是匹配中某条边的一个端点，则称这个点是 **被匹配的 (matched)/饱和的 (saturated)**，否则称这个点是 **不被匹配的 (unmatched)**。

边数最多的匹配被称作一张图的 **最大匹配 (maximum-cardinality matching)**。图 $G$ 的最大匹配的大小记作 $\nu(G)$。

如果边带权，那么权重之和最大的匹配被称作一张图的 **最大权匹配 (maximum-weight matching)**。

如果一个匹配在加入任何一条边后都不再是一个匹配，那么这个匹配是一个 **极大匹配 (maximal matching)**。最大的极大匹配就是最大匹配，任何最大匹配都是极大匹配。极大匹配一定是边支配集，但边支配集不一定是匹配。最小极大匹配和最小边支配集大小相等，但最小边支配集不一定是匹配。求最小极大匹配是 NP 困难的。

如果在一个匹配中所有点都是被匹配的，那么这个匹配是一个 **完美匹配 (perfect matching)**。如果在一个匹配中只有一个点不被匹配，那么这个匹配是一个 **准完美匹配 (near-perfect matching)**。

求一张普通图或二分图的匹配或完美匹配个数都是 #P 完全 的。

对于一个匹配 $M$，若一条路径以非匹配点为起点，每相邻两条边的其中一条在匹配中而另一条不在匹配中，则这条路径被称作一条 **交替路径 (alternating path)**；一条在非匹配点终止的交替路径，被称作一条 **增广路径 (augmenting path)**。

托特定理：$n$ 阶无向图 $G$ 有完美匹配当且仅当对于任意的 $V’ \subset V(G)$，$p_{\text{odd}}(G-V’)\leq |V’|$，其中 $p_{\text{odd}}$ 表示奇数阶连通分支数。

托特定理（推论）：任何无桥 3 - 正则图都有完美匹配。

点覆盖

对于图 $G=(V, E)$，若 $V’\subseteq V$ 且 $\forall e\in E$ 满足 $e$ 的至少一个端点在 $V’$ 中，则称 $V’$ 是图 $G$ 的一个 **点覆盖 (vertex cover)**。

点覆盖集必为支配集，但极小点覆盖集不一定是极小支配集。

一个点集是点覆盖的充要条件是其补集是独立集，因此最小点覆盖的补集是最大独立集。求一张图的最小点覆盖是 NP 困难 的。

一张图的任何一个匹配的大小都不超过其任何一个点覆盖的大小。完全二分图 $K_{n, m}$ 的最大匹配和最小点覆盖大小都为 $\min(n, m)$。

边覆盖

对于图 $G=(V, E)$，若 $E’\subseteq E$ 且 $\forall v\in V$ 满足 $v$ 与 $E’$ 中的至少一条边相邻，则称 $E’$ 是图 $G$ 的一个 **边覆盖 (edge cover)**。

最小边覆盖的大小记作 $\rho(G)$，可以由最大匹配贪心扩展求得：对于所有非匹配点，将其一条邻边加入最大匹配中，即得到了一个最小边覆盖。

最大匹配也可以由最小边覆盖求得：对于最小边覆盖中每对有公共点的边删去其中一条。

一张图的最小边覆盖的大小加上最大匹配的大小等于图的点数，即 $\rho(G)+\nu(G)=|V(G)|$。

一张图的最大匹配的大小不超过最小边覆盖的大小，即 $\nu(G)\le\rho(G)$。特别地，完美匹配一定是一个最小边覆盖，这也是上式取到等号的唯一情况。

一张图的任何一个独立集的大小都不超过其任何一个边覆盖的大小。完全二分图 $K_{n, m}$ 的最大独立集和最小边覆盖大小都为 $\max(n, m)$。

团

对于图 $G=(V, E)$，若 $V’\subseteq V$ 且 $V’$ 中任意两个不同的顶点都相邻，则 $V’$ 是图 $G$ 的一个 **团 (clique)**。团的导出子图是完全图。

如果一个团在加入任何一个顶点后都不再是一个团，则这个团是一个 **极大团 (maximal clique)**。

一张图的最大团的大小记作 $\omega(G)$，最大团的大小等于其补图最大独立集的大小，即 $\omega(G)=\alpha(\bar{G})$。求一张图的最大团是 NP 困难 的。

图的匹配
https://www.lry666.cn/posts/6ec3/
作者
LRY666
发布于
2024年4月15日
许可协议