单调栈单调队列相关题解

单调栈单调队列相关题解

单调栈模板

原题链接：P5788 【模板】单调栈 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

主要思路

本题要求数列中第 $i$ 个元素之后第一个大于$a_i$的元素的下标

我们可以把数组倒过来，那问题便转化为：

数列中第$i$个元素之前最靠后的大于自身的第一个元素在原数组中的下标

我们可以考虑用单调栈来维护一个递减序列，每次碰到一个新元素时，就检查栈顶元素（因为栈顶元素肯定时最靠近自己的有可能满足条件的值）是否大于自身，如果大于，那么输出答案，否则弹出栈顶，继续往前检查，知道栈中无元素为止，如果到最后，也没有找到合法的值，说明数组中没有相应的元素，答案为0

关键代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int main() {
    cin >> n;
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    for (int i = n; i >= 1; i -- ) {
        // 维护单调性
        while (tt && a[stk[tt]] <= a[i]) tt --;
        // 答案数组
        ans[i] = stk[tt];
        // 下标入栈
        stk[++ tt] = i;
    }
    for (int i = 1; i <= n; i ++ ) {
        printf("%d ", ans[i]);
    }
    return 0;
}

单调队列模板

原题链接：P1886 滑动窗口 /【模板】单调队列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

主要思路

求出每次滑动后窗口中的最大值和最小值

我们可以考虑分别求出最大值和最小值，下面先考虑最大值，结论是，最后会形成一个单调递减队列

窗口大小为k，所以，滑出窗口的元素我们要去掉，进入窗口的加入，前后都需要有操作，我们考虑用单调队列，并维护下标。

每次遇到一个新元素

队头操作：先将滑出窗口的元素弹出队列，从队头开始，检查下标是否超出范围，如果超出，则弹出。

队尾操作：与单调栈的模板题类似，如果当前元素大于等于队尾元素，就将队尾弹出，直到队列为空或者队尾元素小于当前元素，此时，插入当前元素，从而形成一个单调递减队列。

完成以上操作之后，队头元素便是窗口中的最大值。

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 10;

int n, k;
int a[N];
int q[N], hh, tt;

int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    // 最大值
    hh = 0, tt = -1;
    for (int i = 1; i <= n; i ++ ) {
        // 维护左端点范围
        while (hh <= tt && i - q[hh] + 1 > k) hh ++;
        // 维护单调性
        while (hh <= tt && a[q[tt]] >= a[i]) tt --;
        // 下标入队
        q[++ tt] = i;
        // 输出答案
        if (i >= k) printf("%d ", a[q[hh]]);
    }
    puts("");
    hh = 0, tt = -1;
    for (int i = 1; i <= n; i ++ ) {
        while (hh <= tt && i - q[hh] + 1 > k) hh ++;
        while (hh <= tt && a[q[tt]] <= a[i]) tt --;
        q[++ tt] = i;
        if (i >= k) printf("%d ", a[q[hh]]);
    }
    puts("");
    return 0;
}

P1901 发射站

原题链接：P1901 发射站 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

主要思路

解题关键：发出的能量只被两边最近的且比它高的发射站接收

也就是说，对于每个发射站，我们要找到两边最近的高度比自身的$H_i$大的发射塔，和我们单调栈的模板一致。本题需要维护两个方向，所以前后分别扫一遍就行了。最终我们维护的是两个单调递减的栈。

AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 10;

int n;
int a[N], b[N];
int stk1[N], stk2[N];
int tt1, tt2;
int val[N];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i ++ ) scanf("%d%d", &a[i], &b[i]);
	
    // 找到离自己最近的，在自己前面的，比自己高的第一个发射塔
    for (int i = 1; i <= n; i ++ ) {
        while (tt1 && a[stk1[tt1]] <= a[i]) tt1 --;
        val[stk1[tt1]] += b[i];
        stk1[++tt1] = i;
    }
	
    // 找到离自己最近的，在自己后面的，比自己高的第一个发射塔
    for (int i = n; i >= 1; i -- ) {
        while (tt2 && a[stk2[tt2]] <= a[i]) tt2 --;
        val[stk2[tt2]] += b[i];
        stk2[++tt2] = i;
    }

    int ans = 0;
    for (int i = 1; i <= n; i ++ ) ans = max(ans, val[i]);
    cout << ans << endl;

    return 0;
}

P2422 良好的感觉

原题链接：P2422 良好的感觉 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

主要思路

解题关键：人的舒适程度定义为 $[i, j]$ 中最不舒服的那一天的感受值$[i, j]$ 中每一天感受值的和

这句话的意思是，对于每个区间$[i,j]$，其产生的贡献是最小值乘上这个区间所有数的总和。

很容易想到，我们试着在不改变区间最小值的前提下，尽可能将区间范围扩大，由于都是非负数，总和一定不会变小，那得出的结果肯定比之前更优。

那么最大能扩大到什么程度呢？显然，扩大到区间的左一个和右一个都比当前区间的最小值小时，这个区间范围最大。

即，找到最近的比该区间的最小值小的那两个数所在的位置，这两个位置之间的数，就是我们能找到的最大范围。

由此，我们想到一个暴力的做法：

枚举每个数为一个区间的最小值，然后向左向右找到区间的左右端点，经过上一题的启发，找端点用单调栈处理。

而区间和又可以用前缀和数组来维护，总的时间复杂度是线性的。

AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 1e5 + 10;

int n;
int a[N];
int stk[N], tt;
int l[N], r[N];
LL s[N];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
	
    // 从前往后扫，找到左边界
    for (int i = 1; i <= n; i ++ ) {
        while (tt && a[stk[tt]] >= a[i]) tt --;
        l[i] = stk[tt] + 1;
        stk[++ tt] = i;
    }
    // 找到有边界
    tt = 0;
    for (int i = n; i >= 1; i -- ) {
        while (tt && a[stk[tt]] >= a[i]) tt --;
        r[i] = stk[tt] - 1;
        stk[++ tt] = i;
    }
	
    // 前缀和
    for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i];

    LL ans = 0;
    for (int i = 1; i <= n; i ++ ) {
        ans = max(ans, a[i] * (s[r[i]] - s[l[i] - 1]));
    }

    cout << ans << endl;

    return 0;
}

P2216 [HAOI2007]理想的正方形

原题链接：[P2216 HAOI2007]理想的正方形 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

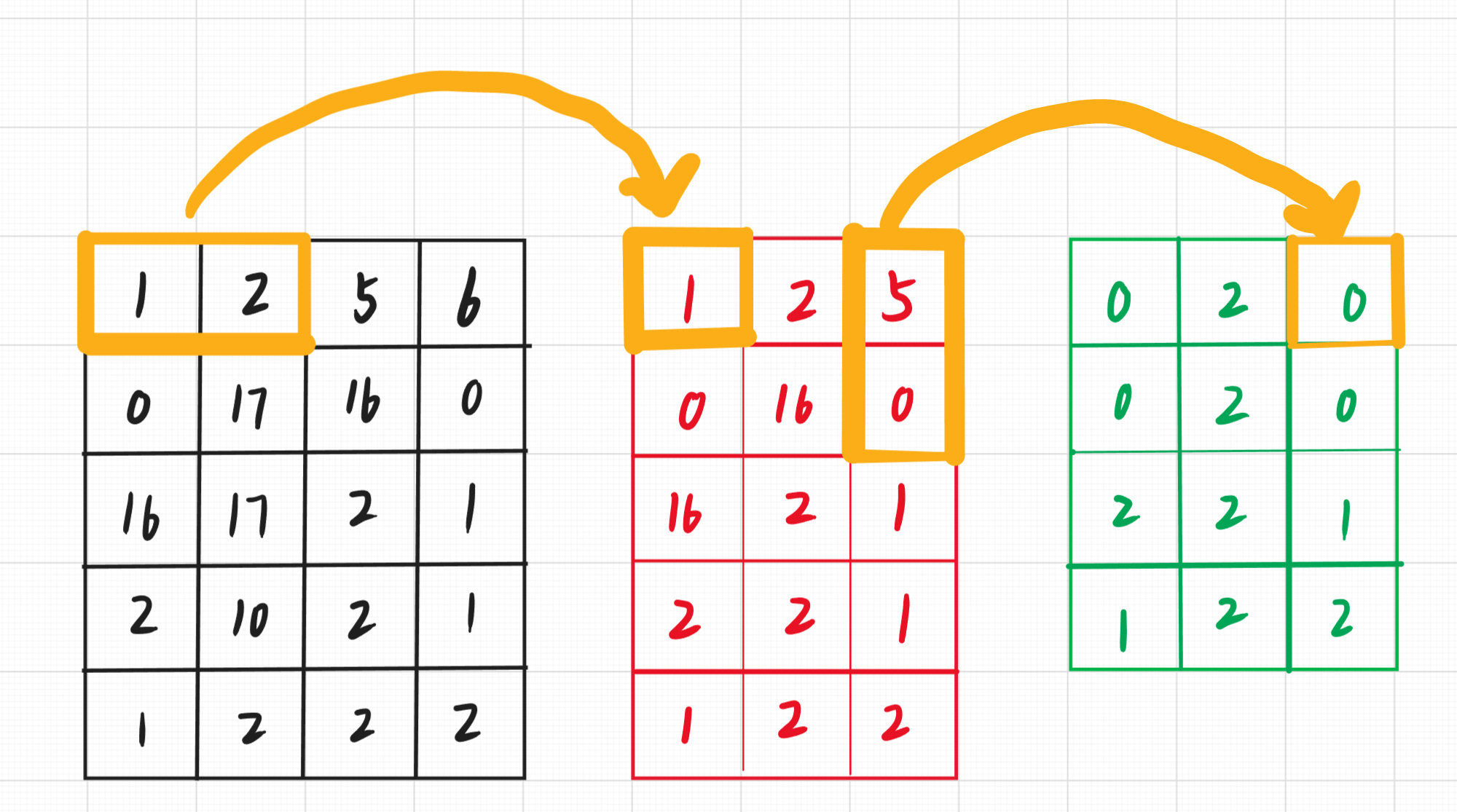
主要思路

考虑暴力做法，求出每个$n \times n$矩阵的最大值和最小值

对于每个矩阵的最值，我们可以先求出每行的最值，这样就能得到一列数据，对于这一列，再求一次最值即可得出这个矩阵的最值。

区间最值问题，可以想到用单调队列优化，我们可以先求出所有行区间的最值，将求得的结果得到一个矩阵，此时，我们对于每个长度为n的子列，再求最值，又可以得到一个更小的矩阵，此时，每个矩阵中的一个点，就对应原矩阵的一个$n \times n$矩阵的一个最值。

对于最大值和最小值，我们分别求出矩阵之后，对两个矩阵中的点做差求最大值即可。

最小值矩阵

复杂度

时间复杂度即为扫5次矩阵大小，$O(n)$

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <bits/stdc++.h>

using namespace std;

const int N = 1010;

int g[N][N];
int a, b, n;
int q[N], hh, tt;
int g1[2][N][N];
int g2[2][N][N];

int main() {
    cin >> a >> b >> n;
    for (int i = 1; i <= a; i ++ )
        for (int j = 1; j <= b; j ++ )
            scanf("%d", &g[i][j]);

    // 最大值
    for (int i = 1; i <= a; i ++ ) {
        hh = 0, tt = -1;
        for (int j = 1; j <= b; j ++ ) {
            while (hh <= tt && j - q[hh] + 1 > n) hh ++;
            while (hh <= tt && g[i][q[tt]] <= g[i][j]) tt --;
            q[++ tt] = j;
            if (j >= n) {
                g1[0][i][j - n + 1] = g[i][q[hh]];
            }
        }
    }
    for (int i = 1; i <= b - n + 1; i ++ ) {
        hh = 0, tt = -1;
        for (int j = 1; j <= a; j ++ ) {
            while (hh <= tt && j - q[hh] + 1 > n) hh ++;
            while (hh <= tt && g1[0][q[tt]][i] <= g1[0][j][i]) tt --;
            q[++ tt] = j;
            if (j >= n) {
                g1[1][j - n + 1][i] = g1[0][q[hh]][i];
            }
        }
    }
    // 最小值
    for (int i = 1; i <= a; i ++ ) {
        hh = 0, tt = -1;
        for (int j = 1; j <= b; j ++ ) {
            while (hh <= tt && j - q[hh] + 1 > n) hh ++;
            while (hh <= tt && g[i][q[tt]] >= g[i][j]) tt --;
            q[++ tt] = j;
            if (j >= n) {
                g2[0][i][j - n + 1] = g[i][q[hh]];
            }
        }
    }
    for (int i = 1; i <= b - n + 1; i ++ ) {
        hh = 0, tt = -1;
        for (int j = 1; j <= a; j ++ ) {
            while (hh <= tt && j - q[hh] + 1 > n) hh ++;
            while (hh <= tt && g2[0][q[tt]][i] >= g2[0][j][i]) tt --;
            q[++ tt] = j;
            if (j >= n) {
                g2[1][j - n + 1][i] = g2[0][q[hh]][i];
            }
        }
    }

    int ans = g1[1][1][1] - g2[1][1][1];
    for (int i = 1; i <= a - n + 1; i ++ ) {
        for (int j = 1; j <= b - n + 1; j ++ ) {
            ans = min(ans, g1[1][i][j] - g2[1][i][j]);
        }
    }

    cout << ans << endl;

    return 0;
}

P2698 [USACO12MAR]Flowerpot S

原题链接：[P2698 USACO12MAR]Flowerpot S - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

主要思路

首先，我们先考虑一下，再不考虑花盆宽度最小的情况下，怎样的花盆符合条件？

假设花盆的左端点为$x_l$右端点为$x_r$，则我们需要满足$max{y_l, y_{l+1}, … , y_{r - 1}, y_r} - min{y_l, y_{l+1}, … , y_{r - 1}, y_r}$的值大于所给的时间$D$。

那么，如何找到宽度最小的花盆呢，暴力的做法是，枚举所有区间，然后找到符合条件的所有花盆里宽度最小的即可。

但是这样的时间复杂度又太高，我们可以考虑用单调队列优化。

之前做过一道滑动窗口的题目，队列的元素的下标是有限制的，但是这题的下标好像并不能限制队列。

而题目中一个明显的限制条件就是时间D，即我们的y数组在一定限制下的最值之差。

于是，我们可以考虑用两个队列分别维护最大值和最小值，并保证这两个队列中的元素的下标范围一致。

这里可以利用一下双指针的思想，当队列中最值之差不符合条件时，将右端点向右移，一旦满足条件之后，尝试将左端点往右移，尝试将盆的宽度尽可能缩小，最终能枚举到所有符合限制$D$的花盆，取一个最小值即可，这里不做严格的论证。

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int n, d;
int x[N], y[N];
int q1[N], q2[N], hh1, tt1, hh2, tt2;
struct Node {
    int x, y;
    bool operator<(const Node &i) {
        return x < i.x;
    }
} a[N];

int main() {
    cin >> n >> d;
    for (int i = 1; i <= n; i ++ ) scanf("%d%d", &a[i].x, &a[i].y);
    sort(a + 1, a + n + 1);

    int ans = 1e7 + 10;
    tt1 = tt2 = -1;
    for (int l = 1, r = 0; l <= n; l ++ ) {
        while (hh1 <= tt1 && q1[hh1] < l) hh1 ++;
        while (hh2 <= tt2 && q2[hh2] < l) hh2 ++;
        while (a[q1[hh1]].y - a[q2[hh2]].y < d && r < n) {
            r ++;
            while (hh1 <= tt1 && a[q1[tt1]].y <= a[r].y) tt1 --;
            q1[++ tt1] = r;
            while (hh2 <= tt2 && a[q2[tt2]].y >= a[r].y) tt2 --;
            q2[++ tt2] = r;
        }
        if (a[q1[hh1]].y - a[q2[hh2]].y >= d) ans = min(ans, a[r].x - a[l].x);
    }

    if (ans >= 1e7) puts("-1");
    else cout << ans << endl;

    return 0;
}

D. Imbalanced Array

原题链接：Problem - 817D - Codeforces

题目大意

题目大意：给你一个序列，让你求出这个序列的每个区间最大值的和 - 最小值的和

主要思路

单调栈经典问题。

我们先求出以 a[ i ] 为最小值的左右最长拓展 L1[i] , R1[i]

那么以 a[ i ] 为最小值的区间个数就为 (L1[ i ] + 1) * (R1[ i ] + 1)

再求出以 a[ i ] 为最大值的左右最长拓展 L2[ i ] , R2[ i ]

那么以 a[ i ] 为最大值的区间个数就为 (L2[ i ] + 1) * (R2[ i ] + 1)

最后线性扫一遍即可

C. Watching Fireworks is Fun

原题链接：Problem - 372C - Codeforces

题目大意

城镇中有 n 个位置，有 m 个烟花要放，每秒钟可以移动 d 长度的距离，每个烟花放出的地点和时间分别为 a[i] 和 t[i] , 如果 在烟花放出时 你所在位置为 j 那么得到的快乐值为 b[i]-abs(j-a[i]) .问你能得到的最大快乐值是多少？

主要思路：

设 看第$i$ 次 烟花时所在位置为 j ，那么 转移方程为 dp[ i ][ j ]=max( dp[ i-1 ][ k ] + b[i] - abs( j - a[i] ) ) , k 的范围为 [ j -d*（t[i]-t[i-1]) , j + d *（t[i]-t[i-1]) ] .
那就等价于 对每一次 烟花 的每一个位置 j 我们都要求 长度为 2 * d * t[i] 区间内的最大值，那么问题又变成 求 滑动窗口内的 最大值。注意这里的窗口长度有左右两部分 。

题解
#栈 #单调栈 #单调队列 #队列 #题解
单调栈单调队列相关题解
https://www.lry666.cn/posts/419d/
作者
LRY666
发布于
2023年1月26日
许可协议